Cauchy inequality

Liouville’s theorem and fundamental theorem of algebra

Proof: Let \(B=\sup_{z\in\mathbb C}|f(z)|\). For each \(z_{0} \in \mathbb{C}\) and all \(R>0\), the Cauchy inequality yields \[\left|f^{\prime}\left(z_{0}\right)\right| \leq \frac{B}{R}\ _{\overrightarrow{R\to\infty}} \ 0.\] Thus \(f'(z_0)=0\) and hence \(f\) must be constant as \(\mathbb C\) is connected. $$\tag*{$\blacksquare$}$$

Fundamental theorem of algebra

Proof: If \(P\) has no roots, then \(1 / P(z)\) is a bounded holomorphic function.

• To see this, we can of course assume that \(a_{n} \neq 0\), and write \[\frac{P(z)}{z^{n}}=a_{n}+\left(\frac{a_{n-1}}{z}+\cdots+\frac{a_{0}}{z^{n}}\right) \quad \text{ whenever } \quad z \neq 0.\]

• Since each term in the parentheses goes to 0 as \(|z| \rightarrow \infty\) we conclude that there exists \(R>0\) so that if \(c=\left|a_{n}\right| / 2\), then \[|P(z)| \geq c|z|^{n} \quad \text { whenever }\quad |z|>R.\]

• In particular, \(P\) is bounded from below when \(|z|>R\).

• Since \(P\) is continuous and has no roots in the disc \(|z| \leq R\), it is bounded from below in that disc as well, thereby proving our claim.

• By Liouville’s theorem we then conclude that \(1 / P\) is constant.

• This contradicts our assumption that \(P\) is non-constant and proves the theorem. $$\tag*{$\blacksquare$}$$

Morera’s theorem — converse to the Cauchy theorem

Proof: Let \(V\) be a convex open set in \(\Omega\).

• As in the proof of Cauchy theorem for convex sets, we can construct a primitive \(F \in H(V)\) such that \(F^{\prime}=f\).

• Fixing \(a\in V\) it suffices to take \[F(z)=\int_{[a, z]} f(\zeta) d \zeta \quad \text{ for }\quad z \in V.\]

• Observe that \([a, z]\subseteq V\) since \(V\) is convex. Let \(z_{0} \in V\), then \[\begin{aligned} F(z)-F\left(z_{0}\right)&=\int_{[a, z]} f(\zeta) d \zeta-\int_{\left[a, z_{0}\right]} f(\zeta) d \zeta\\ &=\int_{\left[z_{0}, z\right]} f(\zeta) d \zeta. \end{aligned}\]

• Hence, we obtain \[\frac{F(z)-F\left(z_{0}\right)}{z-z_{0}}-f\left(z_{0}\right)=\frac{1}{z-z_{0}} \int_{\left[z_{0}, z\right]}\left(f(\zeta)-f\left(z_{0}\right)\right) d \zeta,\] which implies

  \[F'(z_0)=\lim_{z\to z_0}\frac{F(z)-F\left(z_{0}\right)}{z-z_{0}}=f\left(z_{0}\right).\]

• Since derivatives of holomorphic functions are holomorphic, we have \(f \in H(V)\), for every convex open \(V \subseteq \Omega\), hence \(f \in H(\Omega)\). $$\tag*{$\blacksquare$}$$

Sequences of holomorphic functions

Proof: The function \(f\) is continuous, since the convergence is uniform on each compact disc in \(\Omega\). Let \(\Delta\) be a triangle in \(\Omega\). Then \(\Delta\) is compact, so

\[\int_{\partial \Delta} f(z) d z=\lim _{j \rightarrow \infty} \int_{\partial \Delta} f_{j}(z) d z=0\]

by Cauchy’s theorem. Hence Morera’s theorem implies that \(f \in H(\Omega)\).

• Let \(K \subseteq \Omega\) be compact. There exists an \(r>0\) such that the union \(E\) of the closed discs \(\overline{D}(z ; r)\), for all \(z \in K\), is a compact subset of \(\Omega\).

• Applying Cauchy’s inequality to \(f-f_{j}\), we have \[\left|f^{\prime}(z)-f_{j}^{\prime}(z)\right| \leq r^{-1}\left\|f-f_{j}\right\|_{L^{\infty}(E)} \quad\text{ for } \quad z \in K,\] where \(\|f\|_{L^\infty(E)}=\sup_{z\in E}|f(z)|\). Since \(\lim_{j\to \infty}f_{j} = f\) uniformly on \(E\), it follows that \(f_{j}^{\prime} \rightarrow f^{\prime}\) uniformly on \(K\).

• Compare this with the situation on the real line, where sequences of infinitely differentiable functions can converge uniformly to nowhere differentiable functions!

Zero sets of holomorphic functions

Proof: Let \(A\) be the set of all limit points of \(Z(f)\) in \(\Omega\). In other words, \[A=\{z\in\mathbb C: \exists_{(z_n)_{n\in\mathbb N}\subseteq Z(f)} \ z_n\neq z\ \text{ and } \lim_{n\to \infty}z_n=z\}.\]

• Since \(f\) is continuous, then \(A \subseteq Z(f)\). Indeed, if \(z\in A\) then there \((z_n)_{n\in\mathbb N}\subseteq Z(f)\) such that \(z_n\neq z\) and \(\lim_{n\to \infty}z_n=z\). By continuity of \(f\) we obtain that \(f(z)=\lim_{n\to \infty}f(z_n)=0\).

• We will show that \(A\) is closed in \(\Omega\). Indeed, if \((z_n)_{n\in\mathbb N}\subseteq A\) and \(\lim_{n\to \infty}z_n=z_0\), then for any \(\varepsilon>0\) there exists \(N_{\varepsilon}\in\mathbb N\) such that \(z_n\in D(z_0, \varepsilon)\) for all \(n \ge N_{\varepsilon}\). Since \(z_n\) is a limit point of \(Z(f)\), then \(D(z_0, \varepsilon)\) contains infinitely many points of \(Z(f)\) different from \(z_n\), and hence infinitely many points of \(Z(f)\) different from \(z_0\). Thus \(z_0\in A\).

• This shows that \(A\) is closed.

• Fix \(a \in Z(f)\), and choose \(r>0\) so that \(D(a ; r) \subseteq \Omega\), then \[f(z)=\sum_{n=0}^{\infty} c_{n}(z-a)^{n} \quad \text{ for } \quad z \in D(a ; r).\]

• There are now two possibilities:

  • Either \(c_{n}=0\) for all integers \(n\ge0\);

  • Or there is a smallest integer \(m\) (necessarily positive, since \(f(a)=0=c_0\)) such that \(c_{m} \neq 0\).

• In that case, we can define \[g(z)= \begin{cases}(z-a)^{-m} f(z) & \text{ if } z \in \Omega\setminus\{a\}, \\ c_{m} & \text{ if } z=a. \end{cases}\]

• It is clear that \(g \in H(\Omega\setminus\{a\})\).

• Moreover, for \(z \in D(a ; r)\), we have \[f(z)=(z-a)^{m}g(z)=(z-a)^{m}\Big(c_m+\sum_{n=1}^{\infty} c_{n+m}(z-a)^{n}\Big),\tag{**}\] where \[g(z)=\sum_{n=0}^{\infty} c_{n+m}(z-a)^{n} \quad\text{ for } \quad z \in D(a ; r).\]

• Since \(g \in H(D(a ; r))\), we consequently conclude that \(g \in H(\Omega)\).

• Hence we obtain the factorization from (*) for some \(g \in H(\Omega)\), i.e. \[f(z)=(z-a)^{m} g(z) \quad \text{ for } \quad z \in \Omega.\]

• Moreover, \(g(a)=c_m \neq 0\), and the continuity of \(g\) shows that there is a neighborhood of \(a\) in which \(g\) has no zero, by (**).

• Thus we have shown that \(a\) is an isolated point of \(Z(f)\).

• If \(a \in A\), and \(a\) is a limit point of \(Z(f)\) then the first case (i) must occur and all coefficients \(c_{n}\) are \(0\), then \(f(z)=0\) for all \(z \in D(a ; r)\), and consequently \(D(a ; r) \subseteq A\) and \(a\) is an interior point of \(A\).

• This proves that \(A\) is open.

• If \(B=\Omega\setminus A\), then \(B\) is open.

• Thus \(\Omega\) is the union of the disjoint open sets \(A\) and \(B\).

• Since \(\Omega\) is connected, we have

  • either \(A=\Omega\), in which case \(Z(f)=\Omega\),

  • or \(A=\varnothing\).

• In the latter case, \(Z(f)\) has at most finitely many points in each compact subset of \(\Omega\), and since \(\Omega\) is \(\sigma\)-compact, \(Z(f)\) is at most countable. $$\tag*{$\blacksquare$}$$

Identity theorem

Symmetry principle

Let \(\Omega\) be an open subset of \(\mathbb{C}\) that is symmetric with respect to the real line, that is \[z \in \Omega \quad \text { if and only if } \quad \bar{z} \in \Omega .\]

Let \(\Omega^{+}\)denote the part of \(\Omega\) that lies in the upper half-plane and \(\Omega^{-}\) that part that lies in the lower half-plane.

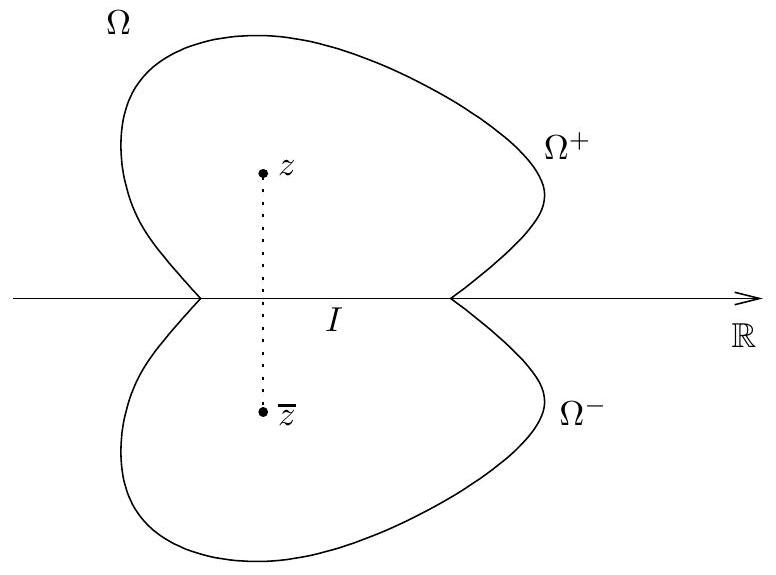
Also, let \(I=\Omega \cap \mathbb{R}\) so that \(I\) denotes the interior of that part of the boundary of \(\Omega^{+}\)and \(\Omega^{-}\)that lies on the real axis. Then we have \[\Omega^{+} \cup I \cup \Omega^{-}=\Omega.\]

Proof: One notes first that \(f\) is continuous throughout \(\Omega\). The only difficulty is to prove that \(f\) is holomorphic at points of \(I\). Suppose \(D\) is a disc centered at a point on \(I\) and entirely contained in \(\Omega\). We prove that \(f\) is holomorphic in \(D\) by Morera’s theorem.

• Suppose \(T\) is a triangle in \(D\). If \(T\) does not intersect \(I\), then \[\int_{T} f(z) d z=0,\] since \(f\) is holomorphic in the upper and lower half-discs.

• Suppose now that one side or vertex of \(T\) is contained in \(I\), and the rest of \(T\) is in, say, the upper half-disc.

  

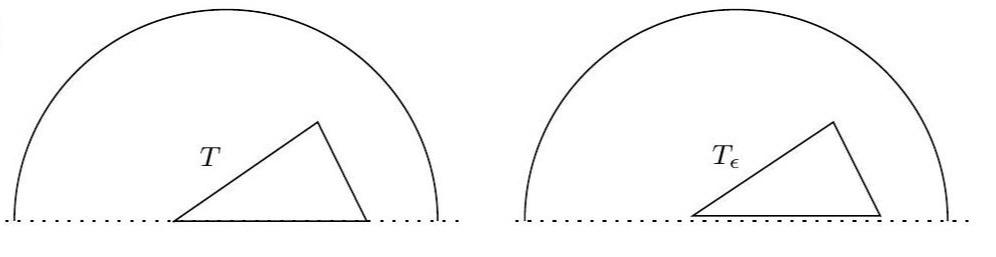
• If \(T_{\epsilon}\) is the triangle obtained from \(T\) by slightly raising the edge or vertex which lies on \(I\), we have \(\int_{T_{\epsilon}} f(z) d z=0,\) since \(T_{\epsilon}\) is entirely contained in the upper half-disc. We then let \(\epsilon \rightarrow 0\), and by continuity we conclude that \[\int_{T} f(z) d z=0.\]

• If the interior of \(T\) intersects \(I\), like below

  

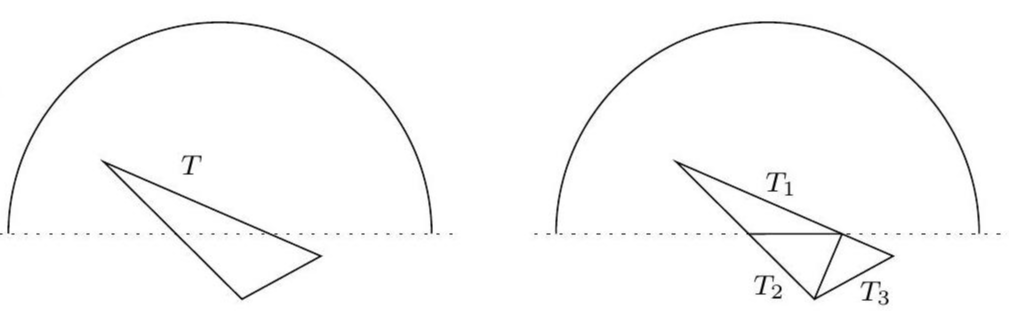
  we can reduce the situation to the previous one by writing \(T\) as the union of triangles each of which has an edge or vertex on \(I\). By Morera’s theorem \(f\) is holomorphic in \(D\), as desired. $$\tag*{$\blacksquare$}$$

Schwarz reflection principle

Proof. The idea is simply to define \(F(z)\) for \(z \in \Omega^{-}\)by \(F(z)=\overline{f(\overline{z})}\)

• To prove that \(F\) is holomorphic in \(\Omega^{-}\)we note that if \(z, z_{0} \in \Omega^{-}\), then \(\overline{z}, \overline{z_{0}} \in \Omega^{+}\)and hence, the power series expansion of \(f\) near \(\overline{z_{0}}\) gives \[f(\overline{z})=\sum a_{n}\left(\overline{z}-\overline{z_{0}}\right)^{n}.\]

• As a consequence we see that \(F\) is holomorphic in \(\Omega^{-}\), since \[F(z)=\sum \overline{a_{n}}\left(z-z_{0}\right)^{n}.\]

• Since \(f\) is real valued on \(I\) we have \(\overline{f(x)}= f(x)\) whenever \(x \in I\) and hence \(F\) extends continuously up to \(I\).

• The proof is complete once we invoke the symmetry principle. $$\tag*{$\blacksquare$}$$

Riemann’s theorem on removable singularities

Proof: Define \[h(z)= \begin{cases} (z-a)^{2} f(z) & \text{ if } z\in \Omega\setminus\{a\},\\ 0 & \text{ if } z=a. \end{cases}\]

• Our boundedness assumption shows that \[h^{\prime}(a)=\lim_{z\to a}\frac{h(z)-h(a)}{z-a}=\lim_{z\to a}(z-a) f(z)=0.\]

• Since \(h\) is evidently differentiable at every other point of \(\Omega\), we have \(h \in H(\Omega)\). Moreover, \(h(a)=h'(a)=0\), so \[h(z)=\sum_{n=2}^{\infty} c_{n}(z-a)^{n} \quad \text{ for } \quad z \in D(a ; r).\]

• We obtain the desired holomorphic extension of \(f\) by setting \(f(a)=c_{2}\), for then \[f(z)=\sum_{n=0}^{\infty} c_{n+2}(z-a)^{n} \quad \text{ for } \quad z \in D(a ; r). \qquad \tag*{$\blacksquare$}\]

Singularities

Proof: Suppose (c) fails.

• Then there exist \(r>0\), and \(\delta>0\), and \(w\in\mathbb C\) such that \[|f(z)-w|>\delta\quad \text{ for all } \quad z\in D^{\prime}(a ; r).\]

• Let us write \(D\) for \(D(a ; r)\) and \(D^{\prime}\) for \(D^{\prime}(a ; r)\). Define

  \[g(z)=\frac{1}{f(z)-w} \quad \text{ for } \quad z \in D^{\prime}. \tag{1}\]

• Then \(g \in H\left(D^{\prime}\right)\) and \(|g|<1 / \delta\). Since \(g\) is bounded, then by the previous theorem it extends to a holomorphic function in \(D\).

• If \(g(a) \neq 0,\) then formula (1) shows that \(f\) is bounded in \(D^{\prime}(a ; \rho)\) for some \(\rho>0\).

• Hence, by the previous theorem \(f\) can be extended to a holomorphic function in \(D(a ; \rho)\), and consequently holomorphic in \(\Omega\), yielding (a).

• If \(g\) has a zero of order \(m \geq 1\) at \(a\), then we can write \[g(z)=(z-a)^{m} g_{1}(z) \quad \text{ for } \quad z \in D, \tag{2}\] where \(g_{1} \in H(D)\) and \(g_{1}(a) \neq 0\). Also, \(g_{1}\) has no zero in \(D^{\prime}\), by (1).

• Thus we can set \(h=\) \(1 / g_{1}\) in \(D\).

• Then \(h \in H(D)\), and \(h\) has no zero in \(D\), and we can write \[f(z)-w=(z-a)^{-m} h(z) \quad \text{ for } \quad z \in D^{\prime}. \tag{3}\]

• But \(h\) has an expansion of the form \[h(z)=\sum_{n=0}^{\infty} b_{n}(z-a)^{n} \quad \text{ for } \quad z \in D, \tag{4}\] with \(b_{0} \neq 0\).

• Identity (3) shows that (b) holds, with \(c_{k}=b_{m-k}\) for \(k=1, \ldots, m\).

• This completes the proof.$$\tag*{$\blacksquare$}$$

Remarks.

Suppose \(f\) has an isolated singularity at \(z_{0}\), and let \[\sum_{n=-\infty}^{\infty} a_{n}\left(z-z_{0}\right)^{n}\] be the Laurent expansion of \(f\) about \(z_{0}\). Then one can see that

• \(f\) has a removable singularity at \(z_{0}\) if \(a_{n}=0\) for all \(n<0\).

• \(f\) has a pole of order \(m\) at \(z_{0}\) if \(m\) is the largest positive integer such that \(a_{-m} \neq 0\). (A pole of order \(1\) is called a simple pole.)

• Finally, if \(a_{n} \neq 0\) for infinitely many \(n<0\), we say that \(f\) has an essential singularity at \(z_{0}\).

• The behavior of a complex function \(f\) at \(\infty\) may be studied by considering \(g(z)= f(1 / z)\) for \(z\) near \(0\). Then we say that \(f\) has an isolated singularity at \(\infty\) if \(f\) is analytic on \(\{z\in \mathbb C:|z|>r\}\) for some \(r\); thus the function \(g(z)=f(1 / z)\) has an isolated singularity at \(0\). The type of singularity of \(f\) at \(\infty\) is then defined as that of \(g\) at \(0\).