Jensen’s formula

The proof of the theorem consists of several steps.

• Step 1. First, we observe that if \(f_{1}\) and \(f_{2}\) are two functions satisfying the hypotheses and the conclusion of the theorem, then the product \(f_{1}f_{2}\) also satisfies the hypothesis of the theorem and formula (*).

• This is a simple consequence of the fact that \(\log x y=\log x+\log y\) whenever \(x, y\in\mathbb R_+\), and that the set of zeros of \(f_{1}f_{2}\) is the union of the sets of zeros of \(f_{1}\) and \(f_{2}\).

• Step 2. The function \[g(z)=\frac{f(z)}{\left(z-z_{1}\right) \cdots\left(z-z_{N}\right)}\] initially defined on \(\Omega\setminus\left\{z_{1}, \ldots, z_{N}\right\}\), is bounded near each \(z_{j}\).

• Therefore each \(z_{j}\) is a removable singularity, and hence we can write \[f(z)=\left(z-z_{1}\right) \cdots\left(z-z_{N}\right) g(z),\] where \(g\) is holomorphic in \(\Omega\) and nowhere vanishing in the closure of \(D(0, R)\). By Step 1, it suffices to prove Jensen’s formula for functions like \(g\) that vanish nowhere, and for functions of the form \(z-z_{j}\).

• Step 3. We first prove (*) for a function \(g\) that vanishes nowhere in the closure of \(D(0, R)\). More precisely, we must establish the following identity: \[\begin{aligned} \log |g(0)|=\frac{1}{2 \pi} \int_{0}^{2 \pi} \log |g(R e^{i \theta})| d \theta. \end{aligned}\tag{**}\]

• In a slightly larger disc, we can write \(g(z)=e^{h(z)}\) where \(h\) is holomorphic in that disc. This is possible since discs are simply connected, and we can define \(h=\log g\).

• Now \[|g(z)|=|e^{h(z)}|=|e^{\operatorname{Re}(h(z))+i \operatorname{Im}(h(z))}|=e^{\operatorname{Re}(h(z))},\] so that \(\log |g(z)|=\operatorname{Re}(h(z))\). Then the mean value property for holomorphic functions (in our case with \(h=\log g\)) immediately implies the desired formula for its real part, which is precisely (**).

• Step 4. The last step is to prove the formula for functions of the form \(f(z)=z-w\), where \(w \in D(0, R)\). That is, we must show that \[\log |w|=\log \left(\frac{|w|}{R}\right)+\frac{1}{2 \pi} \int_{0}^{2 \pi} \log |R e^{i \theta}-w| d \theta.\]

• Since \(\log (|w| / R)=\log |w|-\log R\) and \[\log|R e^{i \theta}-w|=\log R+\log |e^{i \theta}-w / R|,\]

  it suffices to prove that \[\int_{0}^{2 \pi} \log |e^{i \theta}-a| d \theta=0, \quad \text { whenever } \quad |a|<1.\]

• This in turn is equivalent (after the change of variables \(\theta \mapsto-\theta\) ) to \[\int_{0}^{2 \pi} \log |1-a e^{i \theta}| d \theta=0, \quad \text { whenever } \quad |a|<1.\]

• To prove this, we use the function \(F(z)=1-a z\), which vanishes nowhere in the closure of the unit disc.

• As a consequence, there exists a holomorphic function \(G\) in a disc of radius greater than \(1\) such that \[F(z)=e^{G(z)}.\]

• Then \(|F|=e^{\operatorname{Re}(G)}\), and therefore \(\log |F|=\operatorname{Re}(G)\). Since \(F(0)=1\) we have \(\log |F(0)|=0\), and an application of the mean value property to the real part of holomorphic function \(G\), which is \(\log |F(z)|\) concludes the proof of the theorem, giving \[\int_{0}^{2 \pi} \log |1-a e^{i \theta}| d \theta=0, \quad \text { whenever } \quad |a|<1.\qquad \tag*{$\blacksquare$}\]

• From Jensen’s formula we can derive an identity linking the growth of a holomorphic function with its number of zeros inside a disc.

• If \(f\) is a holomorphic function on the closure of a disc \(D(0, R)\), we denote by \(\mathfrak{n}_{f}(r)\) the number of zeros of \(f\) (counted with their multiplicities) inside the disc \(D(0, r)\), with \(0<r<R\).

• A simple but useful observation is that \(\mathfrak{n}_{f}(r)\) is a non-decreasing function of \(r\).

Proof:

• First we have \[\sum_{k=1}^{N} \log \left|\frac{R}{z_{k}}\right|=\sum_{k=1}^{N} \int_{\left|z_{k}\right|}^{R} \frac{d r}{r}.\]

• If we define the characteristic function \[\eta_{k}(r)= \begin{cases}1 & \text { if } r>\left|z_{k}\right|, \\ 0 & \text { if } r \leq\left|z_{k}\right|, \end{cases}\] then

  \[\sum_{k=1}^{N} \eta_{k}(r)=\mathfrak{n}_f(r).\]

• The lemma is proved using \[\sum_{k=1}^{N} \int_{\left|z_{k}\right|}^{R} \frac{d r}{r}=\sum_{k=1}^{N} \int_{0}^{R} \eta_{k}(r) \frac{d r}{r}=\int_{0}^{R}\left(\sum_{k=1}^{N} \eta_{k}(r)\right) \frac{d r}{r}=\int_{0}^{R} \mathfrak{n}_f(r) \frac{d r}{r}.\]

• This completes the proof of the lemma. $$\tag*{$\blacksquare$}$$

Functions of finite order

• Let \(f\) be an entire function. If there exist \(\rho\in\mathbb R_+\) and constants \(A, B\in\mathbb R_+\) such that \[|\:f(z)| \leq A e^{B|z|^{\rho}} \quad \text { for all } \quad z \in \mathbb{C},\] then we say that \(f\) has an order of growth \(\leq \rho\).

• We define the order of growth of \(f\) as \[\rho_{f}=\inf \rho,\] where the infimum is taken over all \(\rho>0\) such that \(f\) has an order of growth \(\leq \rho\).

• For example, the order of growth of the function \(e^{z^{2}}\) is \(2\).

Proof: It suffices to prove the estimate for \(\mathfrak{n}_f(r)\) when \(f(0) \neq 0\).

• Indeed, consider \(F(z)=f(z) / z^{l}\), where \(l\) is the order of the zero of \(f\) at the origin. Then \(\mathfrak{n}_{f}(r)\) and \(\mathfrak{n}_{F}(r)\) differ only by a constant, and \(F\) also has an of order of growth \(\leq \rho\).

• If \(f(0) \neq 0\) we may use formula from the previous corollary, namely \[\int_{0}^{R} \mathfrak{n}_f(x) \frac{d x}{x}=\frac{1}{2 \pi} \int_{0}^{2 \pi} \log |\: f(R e^{i \theta})| d \theta-\log|\:f(0)|.\]

• Choosing \(R=2 r\), this formula implies \[\int_{r}^{2 r} \mathfrak{n}_f(x) \frac{dx}{x} \leq \frac{1}{2 \pi} \int_{0}^{2 \pi} \log |\: f(R e^{i \theta})| d \theta-\log |\: f(0)|.\]

• On the one hand, since \(\mathfrak{n}_f(r)\) is increasing, we have \[\int_{r}^{2 r} \mathfrak{n}_f(x) \frac{d x}{x} \geq \mathfrak{n}_f(r) \int_{r}^{2 r} \frac{d x}{x}=\mathfrak{n}_f(r)[\log 2 r-\log r]=\mathfrak{n}_f(r) \log 2.\]

• On the other hand, the growth condition on \(f\) (for all large \(r\)) gives \[\int_{0}^{2 \pi} \log |f(R e^{i \theta})| d \theta \leq \int_{0}^{2 \pi} \log |A e^{B R^{\rho}}| d \theta \leq C^{\prime} r^{\rho}.\]

• Consequently, \(\mathfrak{n}_f(r) \leq C r^{\rho}\) for an appropriate \(C>0\) and all sufficiently large \(r\).

• The following estimates prove the second part of the theorem: \[\begin{aligned} \sum_{\left|z_{k}\right| \geq 1}\left|z_{k}\right|^{-s} & =\sum_{j=0}^{\infty}\left(\sum_{2^{j} \leq\left|z_{k}\right|<2^{j+1}}\left|z_{k}\right|^{-s}\right) \\ & \leq \sum_{j=0}^{\infty} 2^{-j s} \mathfrak{n}_f\left(2^{j+1}\right) \\ & \leq c \sum_{j=0}^{\infty} 2^{-j s} 2^{(j+1) \rho} \leq c^{\prime} \sum_{j=0}^{\infty}\left(2^{\rho-s}\right)^{j} <\infty \end{aligned}\]

• The last series converges because \(s>\rho\).

This completes the proof of the theorem.$$\tag*{$\blacksquare$}$$

Infinite products

• Given a sequence \((a_{n})_{n\in\mathbb Z_+}\subseteq \mathbb C\), we say that the product \[\prod_{n=1}^{\infty}\left(1+a_{n}\right)\] converges if the limit \[\lim _{N \rightarrow \infty} \prod_{n=1}^{N}\left(1+a_{n}\right)\] of the partial products exists.

• A useful necessary condition that guarantees the existence of a product is contained in the following lemma.

• If \(\sum_{n\in\mathbb Z_+}\left|a_{n}\right|\) converges, then for all large \(n\) we must have \(\left|a_{n}\right|<1 / 2\). We may assume, without loss of generality, that this inequality holds for all \(n\in\mathbb Z_+\).

• Hence, we can define \(\log \left(1+a_{n}\right)\) by the usual power series, and this logarithm satisfies the property that \[1+z=e^{\log (1+z)},\] whenever \(|z|<1\).

• Hence we may write the partial products as follows: \[\prod_{n=1}^{N}\left(1+a_{n}\right)=\prod_{n=1}^{N} e^{\log \left(1+a_{n}\right)}=e^{B_{N}}\] where \(B_{N}=\sum_{n=1}^{N} b_{n}\) with \(b_{n}=\log \left(1+a_{n}\right)\).

• By the power series expansion we see that \[|\log (1+z)| \leq 2|z|,\] if \(|z|<1 / 2\). Hence \(\left|b_{n}\right| \leq 2\left|a_{n}\right|\), so \(B_{N}\) converges as \(N \rightarrow \infty\) to a complex number, say \(B\).

• Since the exponential function is continuous, we conclude that \[\lim_{N\to \infty}e^{B_{N}}=e^{B},\] and the first part follows.

• Observe also that if \(1+a_{n} \neq 0\) for all \(n\in\mathbb Z_+\), then the product converges to a non-zero limit since it is expressed as \(e^{B}\). $$\tag*{$\blacksquare$}$$

Infinite products of holomorphic functions

• To prove the first statement, note that for each \(z\) we may argue as in the previous lemma if we write \(F_{n}(z)=1+a_{n}(z)\), with \(\left|a_{n}(z)\right| \leq c_{n}\).

• Then, we observe that the estimates are actually uniform in \(z\) because the \(c_{n}\) ’s are constants. It follows that the product converges uniformly to a holomorphic function, which we denote by \(F(z)\).

• To establish the second part of the theorem, suppose that \(K\) is a compact subset of \(\Omega\), and let \[G_{N}(z)=\prod_{n=1}^{N} F_{n}(z).\]

• We have just proved that \(\lim_{N\to\infty}G_{N} = F\) uniformly in \(\Omega\). Hence, the sequence \((G_{N}^{\prime})_{N\in\mathbb Z_+}\) converges uniformly to \(F^{\prime}\) in \(K\).

• Since \(G_{N}\) is uniformly bounded from below on \(K\), we conclude that \[\lim_{N\to\infty}\frac{G_{N}^{\prime}}{ G_{N}} =\frac{F^{\prime}}{F}\] uniformly on \(K\), and because \(K\) is an arbitrary compact subset of \(\Omega\), the limit holds for every point of \(\Omega\).

• Moreover, a simple calculation yields \[\frac{G_{N}^{\prime}}{G_{N}}=\sum_{n=1}^{N} \frac{F_{n}^{\prime}}{F_{n}},\] so part (ii) of the lemma is also proved. $$\tag*{$\blacksquare$}$$

Canonical factors

• For each integer \(k \geq 0\) we define the canonical factors by \[E_{0}(z)=1-z,\] and \[E_{k}(z)=(1-z) e^{z+z^{2} / 2+\cdots+z^{k} / k}, \quad \text { for } k \geq 1.\] The integer \(k\) is called the degree of the canonical factor.

Proof: If \(|z| \leq 1 / 2\), then with the logarithm defined in terms of the power series, we have \(1-z=e^{\log (1-z)}\).

• Therefore \[E_{k}(z)=e^{\log (1-z)+z+z^{2} / 2+\cdots+z^{k} / k}=e^{w}\] where \(w=-\sum_{n=k+1}^{\infty} z^{n} / n\). Observe that since \(|z| \leq 1 / 2\) we have \[|w| \leq|z|^{k+1} \sum_{n=k+1}^{\infty}|z|^{n-k-1} / n \leq|z|^{k+1} \sum_{j=0}^{\infty} 2^{-j} \leq 2|z|^{k+1}.\]

• In particular, we have \(|w| \leq 1\) and this implies that \[\left|1-E_{k}(z)\right|=\left|1-e^{w}\right| \leq e|w| \leq 2e|z|^{k+1}. \qquad \tag*{$\blacksquare$}\]

Weierstrass infinite products

Proof:

• Recall that if a holomorphic function \(f\) vanishes at \(z=a\), then the multiplicity of the zero \(a\) is the integer \(m\) so that \[f(z)=(z-a)^{m} g(z),\] where \(g\) is holomorphic and nowhere vanishing in a neighborhood of \(a\).

• To begin the proof, note first that if \(f_{1}\) and \(f_{2}\) are two entire functions that vanish at all \(z=a_{n}\) and nowhere else, then \(f_{1} / f_{2}\) has removable singularities at all the points \(a_{n}\). Hence \(f_{1} / f_{2}\) is entire and vanishes nowhere, so that there exists an entire function \(g\) with \[f_{1}(z) / f_{2}(z)=e^{g(z)}.\]

• Therefore \(f_{1}(z)=f_{2}(z) e^{g(z)}\) as desired.

• We have to construct a function that vanishes at all the points of the sequence \((a_{n})_{n\in\mathbb Z_+}\) and nowhere else.

• Suppose that we are given a zero of order \(m\) at the origin, and that \(a_{1}, a_{2} \ldots\) are all non-zero. Then we define the Weierstrass product by \[f(z)=z^{m} \prod_{n=1}^{\infty} E_{n}\left(z / a_{n}\right).\]

• We claim that this function has the required properties; that is,

• \(f\) is entire with a zero of order \(m\) at the origin;

• \(f\) has zeros at each point of the sequence \((a_{n})_{n\in\mathbb Z_+}\);

• \(f\) vanishes nowhere else.

• Fix \(R>0\), and suppose that \(z\) belongs to the disc \(D(0, R)\). We shall prove that \(f\) has all the desired properties in this disc, and since \(R\) is arbitrary, this will prove the theorem.

• We can consider two types of factors in the formula defining \(f\), with the choice depending on whether \(\left|a_{n}\right| \leq 2 R\) or \(\left|a_{n}\right|>2 R\).

• There are only finitely many terms of the first kind, since \[\lim_{n\to\infty}\left|a_{n}\right| =\infty,\] and we see that the finite product vanishes at all \(z=a_{n}\in D(0, R)\).

• If \(\left|a_{n}\right| \geq 2 R\), we have \(\left|z / a_{n}\right| \leq 1 / 2\), hence the previous lemma implies \[\left|E_{n}\left(z / a_{n}\right)-1\right| \leq 2e\left|\frac{z}{a_{n}}\right|^{n+1} \leq \frac{e}{2^{n}}.\]

• Therefore, the product \[\prod_{\left|a_{n}\right| \geq 2 R} E_{n}\left(z / a_{n}\right)\] defines a holomorphic function when \(|z|<R\), and does not vanish in that disc by the previous lemmas.

• This shows that the function \(f\) has the desired properties, and the proof of Weierstrass’s theorem is complete. $$\tag*{$\blacksquare$}$$

Hadamard’s theorem

• We gather a few lemmas needed in the proof of Hadamard’s theorem.

Proof:

• If \(|z| \leq 1 / 2\) we can use the power series to define the logarithm of \(1-z\), so that \[E_{k}(z)=e^{\log (1-z)+\sum_{n=1}^{k} z^{n} / n}=e^{-\sum_{n=k+1}^{\infty} z^{n} / n}=e^{w}.\]

  Since \(\left|e^{w}\right| \geq e^{-|w|}\) and \(|w| \leq c|z|^{k+1}\), the first part follows.

• For the second part, simply observe that if \(|z| \geq 1 / 2\), then \[\left|E_{k}(z)\right|=|1-z|\left|e^{z+z^{2} / 2+\cdots+z^{k} / k}\right|,\] and that there exists \(c^{\prime}>0\) such that \[\left|e^{z+z^{2} / 2+\cdots+z^{k} / k}\right| \geq e^{-\left|z+z^{2} / 2+\cdots+z^{k} / k\right|} \geq e^{-c^{\prime}|z|^{k}}. \qquad \tag*{$\blacksquare$}\]

Proof: First, we write \[\prod_{n=1}^{\infty} E_{k}\left(z / a_{n}\right)=\prod_{\left|a_{n}\right| \leq 2|z|} E_{k}\left(z / a_{n}\right) \prod_{\left|a_{n}\right|>2|z|} E_{k}\left(z / a_{n}\right)\]

• For the second product the estimate asserted above holds for all \(z\in\mathbb C\). Indeed, by the previous lemma \[\begin{aligned} \bigg|\prod_{\left|a_{n}\right|>2|z|} E_{k}\left(z / a_{n}\right)\bigg| & =\prod_{\left|a_{n}\right|>2|z|}\left|E_{k}\left(z / a_{n}\right)\right| \\ & \geq \prod_{\left|a_{n}\right|>2|z|} e^{-c | z / a_{n}|^{k+1}} \geq e^{-c|z|^{k+1} \sum_{\left|a_{n}\right|>2|z|}\left|a_{n}\right|^{-k-1}} . \end{aligned}\]

• But \(\left|a_{n}\right|>2|z|\) and \(s<k+1\), so we must have \[\left|a_{n}\right|^{-k-1}=\left|a_{n}\right|^{-s}\left|a_{n}\right|^{s-k-1} \leq C\left|a_{n}\right|^{-s}|z|^{s-k-1} .\]

• Therefore, the fact that \(\sum_{n\in\mathbb Z_+}\left|a_{n}\right|^{-s}\) converges implies that \[\bigg|\prod_{\left|a_{n}\right|>2|z|} E_{k}\left(z / a_{n}\right)\bigg| \geq e^{-c|z|^{s}}\] for some constant \(c>0\), which may depend on \(k\) and \(s\).

• To estimate the first product, we use the second part of the previous lemma, and write \[\begin{aligned} \bigg|\prod_{\left|a_{n}\right| \leq 2|z|} E_{k}\left(z / a_{n}\right)\bigg| \geq \prod_{\left|a_{n}\right| \leq 2|z|}\bigg|1-\frac{z}{a_{n}}\bigg| \prod_{\left|a_{n}\right| \leq 2|z|} e^{-c\left|z / a_{n}\right|^{k}}. \end{aligned}\tag{*}\]

• We now note that \[\prod_{\left|a_{n}\right| \leq 2|z|} e^{-c\left|z / a_{n}\right|^{k}} =e^{-c|z|^{k} \sum_{\left|a_{n}\right| \leq 2|z|}\left|a_{n}\right|^{-k}},\] and again, we have \(\left|a_{n}\right|^{-k}=\left|a_{n}\right|^{-s}\left|a_{n}\right|^{s-k} \leq C\left|a_{n}\right|^{-s}|z|^{s-k}\).

• This proves that \[\prod_{\left|a_{n}\right| \leq 2|z|} e^{-c^{\prime}\left|z / a_{n}\right|^{k}} \geq e^{-c|z|^{s}}.\]

• The estimate on the first product on the right-hand side of (*) will require the restriction on \(z\) imposed in the statement of the lemma.

• Indeed, whenever \(z\) does not belong to a disc of radius \(\left|a_{n}\right|^{-k-1}\) centered at \(a_{n}\), we must have \(\left|a_{n}-z\right| \geq\left|a_{n}\right|^{-k-1}\).

• Therefore \[\begin{aligned} \prod_{\left|a_{n}\right| \leq 2|z|}\left|1-\frac{z}{a_{n}}\right| & =\prod_{\left|a_{n}\right| \leq 2|z|}\left|\frac{a_{n}-z}{a_{n}}\right| \\ & \geq \prod_{\left|a_{n}\right| \leq 2|z|}\left|a_{n}\right|^{-k-1}\left|a_{n}\right|^{-1} \\ & =\prod_{\left|a_{n}\right| \leq 2|z|}\left|a_{n}\right|^{-k-2} . \end{aligned}\]

• Finally, the estimate for the first product follows from the fact that \[\begin{aligned} (k+2) \sum_{\left|a_{n}\right| \leq 2|z|} \log \left|a_{n}\right| & \leq(k+2) \mathfrak{n}_f(2|z|) \log 2|z| \\ & \leq c|z|^{s} \log 2|z| \\ & \leq c^{\prime}|z|^{s^{\prime}} \end{aligned}\] for any \(s^{\prime}>s\), and the second inequality follows as \(\mathfrak{n}(2|z|) \leq c|z|^{s}\).

• Hence, we have proved that \[\left|\prod_{n=1}^{\infty} E_{k}\left(z / a_{n}\right)\right| \geq e^{-c'|z|^{s'}},\] except possibly when \(z\) belongs to the union of the discs centered at \(a_{n}\) of radius \(\left|a_{n}\right|^{-k-1}\), for \(n\in\mathbb Z_+\).

• Since we restricted \(s\) to satisfy \(s>\rho_{0}\), we can take an initial \(s\) sufficiently close to \(\rho_{0}\), so that the assertion of the lemma is established (with \(s\) being replaced by \(s^{\prime}\)). $$\tag*{$\blacksquare$}$$

Proof:

• Since \(\sum_{n\in\mathbb Z_+}\left|a_{n}\right|^{-k-1}<\infty\), there exists \(N\in\mathbb Z_+\) so that

  \[\sum_{n=N}^{\infty}\left|a_{n}\right|^{-k-1}<1 / 10.\]

• Therefore, given any two consecutive large integers \(L\) and \(L+1\), we can find \(r\in\mathbb R_+\) with \(L \leq r \leq L+1\), such that the circle of radius \(r\) centered at the origin does not intersect the forbidden discs from the previous lemma.

• Otherwise, the union of the intervals \(I_{n}=\big[\left|a_{n}\right|-\frac{1}{\left|a_{n}\right|^{k+1}},\left|a_{n}\right|+\frac{1}{\left|a_{n}\right|^{k+1}}\big]\) (which are of length \(2\left|a_{n}\right|^{-k-1}\)) would cover all the interval \([L, L+1]\).

  

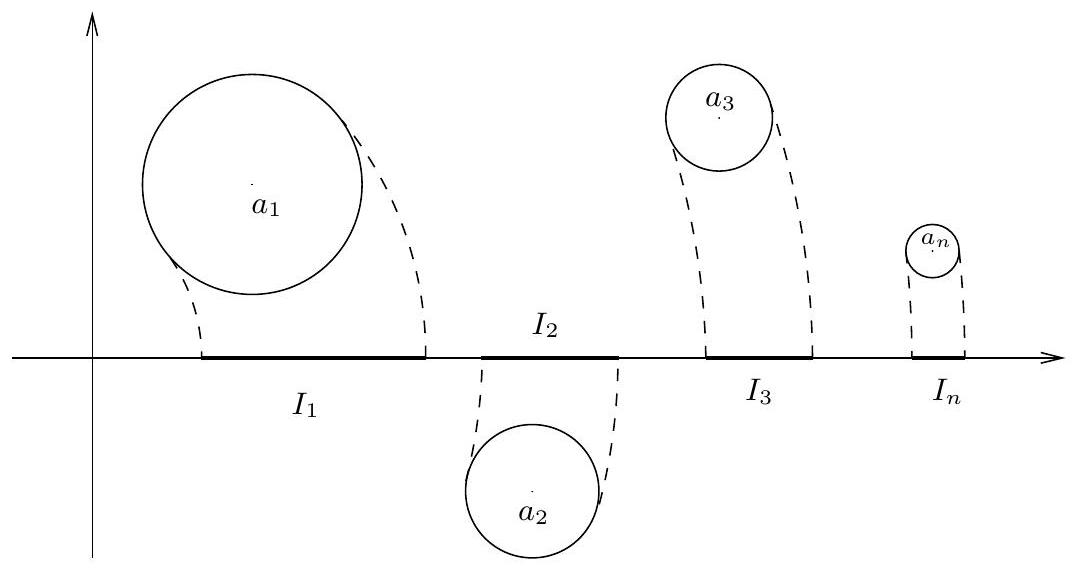
• This would imply \(2 \sum_{n=N}^{\infty}\left|a_{n}\right|^{-k-1} \geq 1\), which is a contradiction. We then apply the previous lemma with \(|z|=r\) and the proof follows. $$\tag*{$\blacksquare$}$$

Proof: Let \[E(z)=z^{m} \prod_{n=1}^{\infty} E_{k}\left(z / a_{n}\right).\]

• To prove that \(E\) is entire, we repeat the argument from the proof of the Weierstrass theorem. Namely, we have \[\left|E_{k}\left(z / a_{n}\right)-1 \right| \leq 2e\left|\frac{z}{a_{n}}\right|^{k+1}, \quad \text { for all large } \quad n\in\mathbb Z_+,\] and that the series \(\sum_{n\in \mathbb Z_+}\left|a_{n}\right|^{-k-1}\) converges. (Here, recall that \(\rho_{0}<s<k+1\).)

• Moreover, \(E\) has the zeros of \(f\), therefore \(f / E\) is holomorphic and nowhere vanishing. Hence \[\frac{f(z)}{E(z)}=e^{g(z)}\] for some entire function \(g\).

• By the fact that \(f\) has growth order \(\rho_{0}\), and because of the estimate from below for \(E\) obtained in the previous corollary, we have \[e^{\operatorname{Re}(g(z))}=\left|\frac{f(z)}{E(z)}\right| \leq c^{\prime} e^{c|z|^{s}}, \quad \text{ whenever } \quad |z|=r_{m}.\]

• This proves that \[\operatorname{Re}(g(z)) \leq C|z|^{s}, \quad \text { for } \quad |z|=r_{m},\] where \((r_m)_{m\in\mathbb Z_+}\subseteq\mathbb R_+\) is a a sequence such that \(\lim_{m\to \infty}r_m=\infty\).

• We have to prove that \(g\) is a polynomial of degree \(\le s\).

• We can expand \(g\) in a power series centered at the origin \[g(z)=\sum_{n=0}^{\infty} a_{n} z^{n}\]

• As a simple application of Cauchy’s integral formulas, we may write \[\frac{1}{2 \pi} \int_{0}^{2 \pi} g\left(r e^{i \theta}\right) e^{-i n \theta} d \theta = \begin{cases} a_{n} r^{n} & \text { if } n \geq 0, \\ 0 & \text { if } n<0. \end{cases}\]

• By taking complex conjugates we find that \[\frac{1}{2 \pi} \int_{0}^{2 \pi} \overline{g\left(r e^{i \theta}\right)} e^{-i n \theta} d \theta=0\] whenever \(n>0\).

• Since \(2 u=g+\overline{g}\) we add the above two equations and obtain \[a_{n} r^{n}=\frac{1}{\pi} \int_{0}^{2 \pi} u\left(r e^{i \theta}\right) e^{-i n \theta} d \theta, \quad \text { whenever } \quad n>0.\]

• For \(n=0\) we find that \[2 \operatorname{Re}\left(a_{0}\right)=\frac{1}{\pi} \int_{0}^{2 \pi} u\left(r e^{i \theta}\right) d \theta.\]

• Now we recall the simple fact that whenever \(n \neq 0\), the integral of \(e^{-i n \theta}\) over any circle centered at the origin vanishes. Therefore \[a_{n}=\frac{1}{\pi r^{n}} \int_{0}^{2 \pi}\left[u\left(r e^{i \theta}\right)-C r^{s}\right] e^{-i n \theta} d \theta \quad \text { when } \quad n>0.\]

• Taking \(r=r_m\), we consequently obtain \[\left|a_{n}\right| \leq \frac{1}{\pi r_m^{n}} \int_{0}^{2 \pi}\left[C r_m^{s}-u\left(r_m e^{i \theta}\right)\right] d \theta \leq 2 C r_m^{s-n}-2 \operatorname{Re}\left(a_{0}\right) r_m^{-n}.\]

• Letting \(m\to \infty\) we deduce \(a_{n}=0\) for any \(n>s\).

• This completes the proof of Hadamard’s theorem. $$\tag*{$\blacksquare$}$$