8. Lebesgue measure in \(\mathbb R^d\) PDF TEX
Lebesgue measure in \(\mathbb R^d\)
Intervals
Recall that-
Let \(J_o\) be the collection of all open intervals in \(\mathbb{R}\): \[J_o=\{(a,b): -\infty \leq a<b \leq \infty\} \cup \{\varnothing\}.\]
-
Let \(J_{co}\) be the collection of all closed-open intervals in \(\mathbb{R}\): \[J_{co}=\{[a,b): -\infty \leq a<b \leq \infty\} \cup \{\varnothing\}.\]
-
Let \(J_{oc}\) be the collection of all open-closed intervals in \(\mathbb{R}\): \[J_{oc}=\{(a,b]: -\infty \leq a<b \leq \infty\} \cup \{\varnothing\}.\]
-
Let \(J_{c}\) be the collection of all closed intervals in \(\mathbb{R}\): \[J_c=\{[a,b]: -\infty \leq a<b \leq \infty\} \cup \{\varnothing\}.\]
-
Let \(J=J_o \cup J_{oc} \cup J_{co} \cup J_c\) be the collection of all intervals in \(\mathbb{R}\).
Euclidean space \(\mathbb{R}^d\)
Let \(\mathbb{R}^d\) be the Euclidean \(d\)-dimensional space with the Euclidean norm \[|x|=\bigg(\sum_{j=1}^{d}|x_j|^2\bigg)^{1/2}=\sqrt{\langle x,x \rangle},\] which is induced by the standard inner product \[\langle x,y \rangle= x\cdot y= \bigg(\sum_{j=1}^{d}x_jy_j\bigg)^{1/2},\] for any \(x=(x_1,\ldots,x_d), y=(y_1,\ldots,y_d)\in\mathbb R^d\).Rectangles
-
open rectangles by \(J_{o}^{d}=\prod_{j=1}^{d}J_o=J_o\times \ldots\times J_o\);
-
closed rectangles by \(J_{c}^{d}=\prod_{j=1}^{d}J_c=J_c\times \ldots\times J_c\);
-
open-closed rectangles by \(J_{oc}^{d}=\prod_{j=1}^{d}J_{oc}=J_{oc}\times \ldots\times J_{oc}\);
-
closed-open rectangles by \(J_{co}^{d}=\prod_{j=1}^{d}J_{co}=J_{co}\times \ldots\times J_{co}\);
Finally we define the family of all rectangles \[\begin{aligned} J^d=J_o^d \cup J_{oc}^d \cup J_{co}^d \cup J^d_c. \end{aligned}\]
Volume function
The open-closed rectangles \(J_{oc}^d\) and closed-open rectangles \(J_{co}^d\) form semi-algebras of sets in \(\mathbb{R}^d\).
Proof. The same as for \(d=1\).$$\tag*{$\blacksquare$}$$
Volume function
For \(I \in J^d\) we define the volume function \({\rm v}_d:J^d \to [0,\infty]\) by \[{\rm v}_d(I)={\rm vol}_d(I)=\begin{cases} 0&\text{ if } I=\varnothing,\\ \prod_{j=1}^{d}(b_j-a_j) &\text{ if } {\rm cl}(I)=\prod_{j=1}^{d}[a_j, b_j],\\ \infty &\text{ otherwise}. \end{cases}\] For \(d=1\) the volume function \({\rm v}_d\) coincides with the length function \(\ell\).
The volume function is finitely additive
A union of rectangles is said to be almost disjoint if the interiors of the rectangles are disjoint.
If \(R=\bigcup_{j=1}^nR_j\in J^d\) and \(R_1,\ldots, R_n \in J^d\) are almost disjoint, then \[{\rm v}_d(R)=\sum_{j=1}^n{\rm v}_d(R_j).\]
Proof. We consider the grid formed by extending indefinitely the sides of all rectangles \(R_1,\ldots,R_n\in J^d\).
-
This extension yields finitely many new rectangles \(\widetilde{R}_1,\ldots,\widetilde{R}_m\in J^d\) and a partition \(J_1,\ldots,J_n\) of the set \(\{1,\ldots, m\}\) such that both unions
\[R=\bigcup_{j=1}^{m}\widetilde{R}_j \quad \text{ and } \quad R_k=\bigcup_{j \in J_k}\widetilde{R}_j \quad \text{ for } \quad k\in\{1,\ldots, n\}\] are almost disjoint.
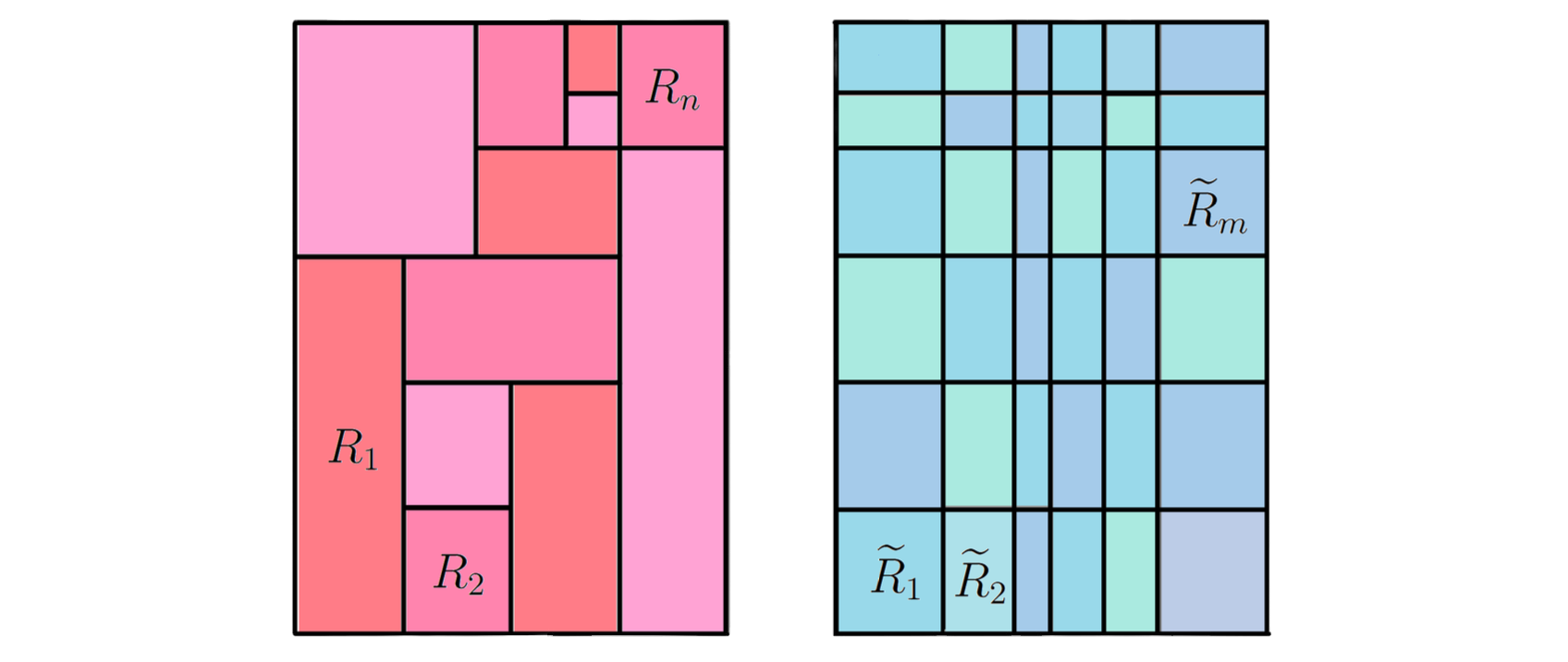
-
For the rectangle \(R\), for example, we see that \[{\rm v}_d(R)=\sum_{j=1}^{m}{\rm v}_d(\widetilde{R}_j)\] since the grid actually partitions the sides of \(R\) and each \(\widetilde{R}_j\) consists of taking products of the intervals in these partitions.
-
Thus when adding the volumes of the \(\widetilde{R}_j\) we are summing the corresponding products of lengths of the intervals that arise. Since this also holds for the other rectangles \(R_1,\ldots, R_n\) we conclude that \[{\rm v}_d(R)=\sum_{j=1}^m {\rm v}_d(\widetilde{R}_j) =\sum_{k=1}^{n}\sum_{j \in J_k}{\rm v}_d(\widetilde{R}_j) =\sum_{k=1}^{n}{\rm v}_d(R_k). \qquad \tag*{$\blacksquare$}\]
Now we proceed as for \(d=1\).
-
We shall be working with \(J_{co}^d\). Let \(\mathcal{A}\) be the algebra of finite disjoint unions of elements from \(J_{co}^d\).
-
It is obvious that \(\sigma(\mathcal{A})=\sigma(J_{co}^d)={\rm Bor}(\mathbb R^d)\).
-
By the previous lemma the volume function \({\rm v}_d\) on \(J_{co}^d\) is finitely additive i.e. for any disjoint family \(R_1,\ldots,R_n\in J_{co}^d\) we have \[{\rm v}_d(R)=\sum_{j=1}^n{\rm v}_d(R_j).\] Thus \({\rm v}_d\) is well defined on \(\mathcal{A}\) as well. We will use the same letter \({\rm v}_d\) to denote the extension to \(\mathcal A\).
-
We have to show that \({\rm v}_d:J_{co}^d \to [0,\infty]\) is countably subadditive on \(J_{co}^d\) then proceeding as for \(d=1\) we conclude that \({\rm v}_d\) is countably additive on \(J_{co}^d\) and its extension to \(\mathcal{A}\) is also countably additive on \(\mathcal{A}\) which means that the volume function \({\rm v}_d\) is a premeasure on \(\mathcal{A}\).
From countably subadditive set functions to premeasures
Theorem (From countably subadditive set functions to premeasures) Let \(\rho:\mathcal{E} \to [0,\infty]\) be a set function on a semi-algebra \(\mathcal{E}\) of subsets of a set \(X\) and \(\rho(\varnothing)=0\). Suppose that \(\rho\) is finitely additive on \(\mathcal{E}\) and let \(\mathcal{A}\) be the algebra that consists of all finite disjoint unions of members of \(\mathcal{E}\). Define a set function \(\mu_0\) on \(\mathcal{A}\) by setting \[\mu_0(A)=\sum_{i=1}^{n}\rho(E_i)\] for \(A=\bigcup_{j=1}^{n}E_j \in \mathcal{A}\), where \(E_1,\ldots,E_n \in \mathcal{E}\) and \(E_i \cap E_j = \varnothing\) if \(i \neq j\).
-
Then \(\mu_0\) is a well-defined additive set function on \(\mathcal{A}\) such that \(\mu_0(\varnothing)=0\) and \(\mu_0=\rho\) on \(\mathcal{E}\).
-
If additionally \(\rho\) is countably subadditive on \(\mathcal{E}\) then \(\mu_0\) is a premeasure on \(\mathcal{A}\).
The volume function is countably subadditive
The volume function \({\rm v}_d:J_{co}^d \to [0,\infty]\) is countably subadditive on \(J_{co}^d\) which immediately implies that \({\rm v}_d\) is countably additive on \(J_{co}^d\).
Proof. The proof is by induction on \(d\). If \(d=1\) then the volume function is the length function \(\ell\), which is countably subadditive on \(J_{co}\). We have to prove that for any \(I \in J_{co}^{d+1}\) and any covering \((I_k)_{k \in \mathbb{N}} \subseteq J^{d+1}_{co}\) so that \[I \subseteq \bigcup_{k \in \mathbb{N}}I_k \in J_{co}^{d+1}\] we have \[{\rm v}_{d+1}(I) \leq \sum_{n \in \mathbb{N}}{\rm v}_{d+1}(I_k).\] The details are left as an exercise.$$\tag*{$\blacksquare$}$$
\(d\)-dimensional Lebesgue measure
-
The \(d\)-dimensional Lebesgue measure \(\lambda_d\) is the restriction of \(\lambda_d^*\) to the Carathéodory \(\sigma\)-algebra \(\mathcal{L}(\mathbb R^d)=\mathcal{M}(\lambda_d^{*})\) of \(\lambda_d^{*}\)-measurable sets.
-
\(\mathcal{L}(\mathbb R^d)=\mathcal{M}(\lambda_d^{*})\) will be called the Lebesgue \(\sigma\)-algebra.
-
The members of \(\mathcal{L}(\mathbb R^d)\) are the Lebesgue measurable sets.
-
By Carathéodory’s theorem \((\mathbb R^d, \mathcal{L}(\mathbb R^d), \lambda_d)\) is a complete measure space. By Carathéodory’s extension theorem \({\rm Bor}(\mathbb R^d)\subseteq \mathcal{L}(\mathbb R^d)\) and \(\lambda_d(I)={\rm v}_d(I)\) for \(I\in J^d=J_o^d \cup J_{oc}^d \cup J_{co}^d \cup J_c^d\) and \(\lambda_d\) is \(\sigma\)-finite on \(\mathbb R^d\). If \(d=1\) we shall abbreviate \(\lambda_d\) to \(\lambda\).
Proposition
Regularity of the Lebesgue measure
-
\(E \in \mathcal L(\mathbb{R}^d)\);
-
For every \(\varepsilon>0\) there exists an open set \(O \supseteq E\) so that \(\lambda_d^{*}(O \setminus E) \leq \varepsilon\);
-
There exists a \(G_{\delta}\)-set \(G \supseteq E\) with \(\lambda_d^{*}(G \setminus E)=0\);
-
For every \(\varepsilon>0\) there exists a closed set \(C \subseteq E\) with \(\lambda_d^*(E \setminus C) \leq \varepsilon\);
-
There exists an \(F_{\sigma}\) set \(F \subseteq E\) with \(\lambda_d^*(E \setminus F)=0\).
Moreover, if \(E \in \mathcal L(\mathbb{R}^d)\), then one has \[\begin{aligned} \lambda_d(E)&=\inf\{\lambda_d(U): U\supseteq E \text{ and } U \text{ is open}\}\\ &=\sup\{\lambda_d(F): F\subseteq E \text{ and } F \text{ is closed}\}\\ &=\sup\{\lambda_d(K): K\subseteq E \text{ and } K \text{ is compact}\}. \end{aligned}\]
Translation invariance of the Lebesgue measure
If \(E\in \mathcal L(\mathbb R^d)\) and \(\lambda_d(E)<\infty\), then for every \(\varepsilon>0\) there is a set \(A\) that is a finite union of open rectangles such that \[\lambda_d(E\triangle A)<\varepsilon.\]
-
For every \(E \subseteq \mathbb{R}^d\) and \(x \in \mathbb{R}^d\) we have \[\lambda_d^{*}(x+E)=\lambda_d^{*}(E),\] where \(x+E=\{x+y:y \in E\}\).
-
For every \(E \in \mathcal{L}(\mathbb{R}^d)\) and \(x \in \mathbb{R}^d\) we have \(x+E \in \mathcal{L}(\mathbb{R}^d)\) and \[\lambda_d(x+E)=\lambda_d(E).\]
Positive homogenity of the Lebesgue measure
-
For \(E \subseteq \mathbb{R^d}\) and \(\alpha \in \mathbb{R}\) we have \[\lambda_d^{*}(\alpha E)=|\alpha|^d\lambda_d^{*}(E),\]
where \(\alpha E=\{\alpha x: x \in E\}\).
-
If \(E \in \mathcal{L}(\mathbb{R}^d)\) and \(\alpha \in \mathbb{R}\) then \(\alpha R \in \mathcal{L}(\mathbb{R}^d)\) and \[\lambda_d(\alpha E)=|\alpha|^d\lambda_d(E).\]
Remark. The proofs go much the same way as for \(d=1\), we omit the details.
Theorem
The Lebesgue measure space \((\mathbb{R}^d,\mathcal{L}(\mathbb{R}^d),\lambda_d)\) is the completion of the Borel measure space \((\mathbb{R}^d,{\rm Bor}(\mathbb{R}^d),\lambda_d)\).
Proof. Let \(\overline{{\rm Bor}(\mathbb{R}^d)}\) be the completion of \({\rm Bor}(\mathbb{R}^d)\) with respect to \(\lambda_d\). i.e. \[\overline{{\rm Bor}(\mathbb{R}^d)}=\{A\cup B \subseteq \mathbb R^d: A\in {\rm Bor}(\mathbb{R}^d) \text{ and } B\subseteq C \in {\rm Bor}_0(\mathbb{R}^d)\},\] where \({\rm Bor}_0(\mathbb{R}^d)=\{C\in {\rm Bor}(\mathbb{R}^d): \lambda_d(C)=0 \}\). Since \((\mathbb{R}^d,\mathcal{L}(\mathbb{R}^d),\lambda_d)\) is complete and \({\rm Bor}(\mathbb{R}^d) \subseteq \mathcal{L}(\mathbb{R}^d)\) thus \[\overline{{\rm Bor}(\mathbb{R}^d)}\subseteq \mathcal{L}(\mathbb{R}^d).\]
Conversely, if \(E \in \mathcal{L}(\mathbb{R}^d)\) then \(E=F\cup N\), where \(F\) is an \(F_\sigma\) set and \(\lambda_d(N)=0\) thus \(E\in \overline{{\rm Bor}(\mathbb{R}^d)}\) and consequently \[\qquad \qquad \mathcal{L}(\mathbb{R}^d) \subseteq \overline{{\rm Bor}(\mathbb{R}^d)}. \qquad \tag*{$\blacksquare$}\]
Metric outer measure spaces
Metric outer measures
Let \((X, \rho)\) be a metric space. An outer measure \(\mu^*\) is called a metric outer measure if \[\mu^*(A\cup B)=\mu^*(A)+\mu^*(B) \quad\text{ whenever } \quad \rho(A, B)>0.\]
Let \(\mu^*\) be an outer measure on a metric space \((X, \rho)\). Then \(\mu^*\) is a metric outer measure if and only if \({\rm Bor}(X)\subseteq \mathcal M(\mu^*)\).
Proof \((\Longrightarrow)\). Let us assume that \(\mu^*\) is a metric outer measure.
Step 1. Since the closed sets generate the Borel \(\sigma\)-algebra \({\rm Bor}(X)\), it suffices to show that every closed set \(F\subseteq X\) is \(\mu^*\) measurable. Thus, given \(A\subseteq X\) with \(\mu^*(A)<\infty\), we have to prove that \[\mu^*(A)\ge \mu^*(A\cap F)+\mu^*(A\cap F^c).\]
Step 2. For each \(n\in \mathbb N\) let \(B_n=\{x\in A\cap F^c: \rho(x, F)\ge n^{-1}\}\). Then \(B_n\subseteq B_{n+1}\) and \[\bigcup_{n\in \mathbb N}B_n=A\cap F^c.\] Indeed, since each \(B_n\subseteq A\cap F^c\) then \(\bigcup_{n\in \mathbb N}B_n\subseteq A\cap F^c.\) Conversely, if \(x\in A\cap F^c\) then \(\rho(x, F)>0\) since \(F\) is closed. Thus there is \(n\in\mathbb N\) such that \(\rho(x, F)\ge n^{-1}\) and consequently \(x\in B_n\) yielding \(A\cap F^c\subseteq \bigcup_{n\in \mathbb N}B_n\).
By the construction of \(B_n\) we also see that \(\rho(B_n, F)\ge n^{-1}\), giving \[\mu^*(A)\ge \mu^*((A\cap F)\cup B_n)\ge \mu^*(A\cap F)+\mu^*(B_n),\] since \(\mu^*\) is a metric outer measure.
It suffices to prove that \[\lim_{n\to \infty}\mu^*(B_n)=\mu^*(A\cap F^c).\]
Step 3. For each \(n\in \mathbb N\) let \(C_n=B_{n+1}\setminus B_{n}\). We claim that \[\rho(C_{n+1}, B_n)\ge \frac{1}{n(n+1)}.\] Indeed, if for some \(x\in C_{n+1}\) and \(y\in B_{n}\) we have \(\rho(x, y)< \frac{1}{n(n+1)}\) then \[\frac{1}{n}\le \rho(y, F)\le \rho(x, y)+\rho(x, F)<\frac{1}{n(n+1)} + \frac{1}{n+1}=\frac{1}{n},\] which is impossible and the claim follows.
A simple induction therefore shows that \[\begin{aligned} \mu^*(B_{2n+1})&\ge \mu^*(C_{2n}\cup B_{2n-1})=\mu^*(C_{2n})+ \mu^*(B_{2n-1})\\ &\ge \mu^*(C_{2n})+ \mu^*(C_{2n-2}\cup B_{2n-3})\\ &=\mu^*(C_{2n})+\mu^*(C_{2n-2})+ \mu^*(B_{2n-3})\ge \sum_{j=1}^n\mu^*(C_{2j}), \end{aligned}\] and similarly one can prove that \(\mu^*(B_{2n})\ge \sum_{j=1}^n\mu^*(C_{2j-1}).\)
Step 4. We have shown that \[\mu^*(B_{2n+1})\ge \sum_{j=1}^n\mu^*(C_{2j}),\qquad \text{ and } \qquad \mu^*(B_{2n})\ge \sum_{j=1}^n\mu^*(C_{2j-1}).\] Since \(\mu^*(B_n)\le \mu^*(A)<\infty\) then \[\sum_{j=1}^{\infty}\mu^*(C_{2j})<\infty, \qquad \text{ and } \qquad \sum_{j=1}^{\infty}\mu^*(C_{2j-1})<\infty.\] By subadditivity, for each \(n\in\mathbb N\), we have that \[\mu^*(A\cap F^c)\le \mu^*(B_n)+\sum_{j=n+1}^{\infty}\mu^*(C_j).\] Passing with \(n\to\infty\) the last sum vanishes and we conclude that \[\mu^*(A\cap F^c)\le \liminf_{n\to\infty}\mu^*(B_n)\le \limsup_{n\to\infty}\mu^*(B_n)\le \mu^*(A\cap F^c).\] This completes the proof of one implication.$$\tag*{$\blacksquare$}$$
Proof \((\Longleftarrow)\). Let us assume that \({\rm Bor}(X)\subseteq \mathcal M(\mu^*)\) and \(\mu^*\) is an outer measure on \(X\). We will show that \(\mu^*\) is a metric outer measure.
-
Let \(A, B\subseteq X\) be such that \(\alpha=\rho(A, B)>0\). Consider an open set \(G_x=\{y\in X: \rho(x, y)<\alpha/2\}\) for every \(x\in X\). Then \[A\subseteq G=\bigcup_{x\in A}G_x.\] Moreover, \(G\) is open and \(G\cap B=\varnothing\).
-
Since \(G\in {\rm Bor}(X)\subseteq \mathcal M(\mu^*)\) we have \[\mu^*(A\cup B)=\mu^*((A\cup B)\cap G)+\mu^*((A\cup B)\cap G^c),\] which implies \[\mu^*(A\cup B)=\mu^*(A)+\mu^*(B).\] since \((A\cup B)\cap G=A\) and \((A\cup B)\cap G^c=B\).$$\tag*{$\blacksquare$}$$
An alternative approach to Lebesgue measure
-
The \(d\)-dimensional Lebesgue measure \(\lambda_d\) is the restriction of \(\lambda_d^*\) to the Carathéodory \(\sigma\)-algebra \(\mathcal{L}(\mathbb R^d)=\mathcal{M}(\lambda_d^{*})\) of \(\lambda_d^{*}\)-measurable sets.
-
\(\mathcal{L}(\mathbb R^d)=\mathcal{M}(\lambda_d^{*})\) will be called the Lebesgue \(\sigma\)-algebra.
-
The members of \(\mathcal{L}(\mathbb R^d)\) are the Lebesgue measurable sets.
-
By Carathéodory’s theorem \((\mathbb R^d, \mathcal{L}(\mathbb R^d), \lambda_d)\) is a complete measure space.
Lebesgue outer measure is a metric outer measure
Remark.
-
In the previous approach we used the Carathéodory extension theorem to prove that
-
\({\rm Bor}(\mathbb R^d)\subseteq \mathcal{L}(\mathbb R^d)\),
-
\(\lambda_d(I)={\rm v}_d(I)\) for \(I\in J^d=J_o^d \cup J_{oc}^d \cup J_{co}^d \cup J_c^d\).
-
-
Here we can proceed differently. Working directly with the Lebesgue outer measure \(\lambda_d^*\) it is a fairly easy exercise to establish that \[\lambda_d^*(I)=\lambda_d(I)={\rm v}_d(I)\] for any \(I\in J^d=J_o^d \cup J_{oc}^d \cup J_{co}^d \cup J_c^d\).
-
To prove that \({\rm Bor}(\mathbb R^d)\subseteq \mathcal{L}(\mathbb R^d)\) we will prove that \(\lambda_d^*\) is a metric outer measure on \(\mathbb R^d\) by appealing to the previous theorem.
Lebesgue outer measure is a metric outer measure
The \(d\)-dimensional Lebesgue outer measure defined for any \(E \subseteq \mathbb{R}^d\) by \[\begin{aligned} \lambda_d^{*}(E)&=\inf\Big\{\sum_{n \in \mathbb{N}}{\rm v}_d(E_n): (E_n)_{n \in \mathbb{N}}\subseteq J_{co}^d\quad \text{ and } \quad E \subseteq \bigcup_{n \in \mathbb{N}}E_n\Big\} \end{aligned}\] is a metric outer measure on \(\mathbb R^d\).
Proof. Let \(E_1, E_2\subseteq \mathbb R^d\) be such that \(\delta=\rho(E_1, E_2)>0\). We have to show that \[\lambda_d^*(E_1\cup E_2)=\lambda_d^*(E_1)+ \lambda_d^*(E_2).\]
-
In fact, by subadditivity we only need to show that \[\lambda_d^*(E_1\cup E_2)\ge \lambda_d^*(E_1)+ \lambda_d^*(E_2).\]
-
It suffices to show that for every sequence \((R_n)_{k\in\mathbb N}\subseteq J_{co}^d\) such that \(\bigcup_{k\in\mathbb N}R_k\supseteq E_1\cup E_2\) we have \[\sum_{k\in \mathbb N}{\rm v}_d(R_k)\ge \lambda_d^*(E_1)+ \lambda_d^*(E_2).\] If \({\rm v}_d(R_k)=\infty\) for some \(k\in\mathbb N\) then there is nothing to prove.
-
We may assume that \({\rm v}_d(R_k)<\infty\) for every \(k\in\mathbb N\). Now for each \(k\in \mathbb N\) each rectangle \(R_k\) can be decomposed into finitely many closed-open rectangles \(\{R_{k, j}:j\in\{1,\ldots, m_k\}\}\subset J_{co}^d\) with the property that
-
\(\{R_{k, j}:j\in\{1,\ldots, m_k\}\}\) is a disjoint collection and \(R_k=\bigcup_{j=1}^{m_k}R_{k, j}\);
-
the lengths of the edges of \(R_{k, 1}, \ldots, R_{k, m_k}\) are all bounded above by \[\delta(2\sqrt{d})^{-1}.\]
-
-
Note that \[{\rm v}_d(R_k)=\sum_{j=1}^{m_k}{\rm v}_d(R_{k, j})\] and let \(\mathcal Q= \{Q_n:n\in\mathbb N\}\) be an arbitrary enumeration of the set \(\{R_{k, j}: k\in\mathbb N \text{ and } j\in\{1,\ldots, m_k\} \}\). Then \[\sum_{n\in\mathbb N}{\rm v}_d(Q_n)=\sum_{k\in\mathbb N}\sum_{j_k=1}^{m_k}{\rm v}_d(R_{k, j_k})=\sum_{k\in\mathbb N}{\rm v}_d(R_{k}).\]
-
Our claim is that no member of \(\mathcal Q\) intersects both \(E_1\) and \(E_2\). Suppose for a contradiction that there is \(n\in\mathbb N\) such that \[Q_n\cap E_1\neq\varnothing \quad \text{ and } \quad Q_n\cap E_2\neq\varnothing.\]
-
Let \(x_1\in Q_n\cap E_1\) and \(x_2\in Q_n\cap E_2\) and note that \[\delta=\rho(E_1, E_2)\le \rho(x_1, x_2)\le \Big(d\big(\delta(2\sqrt{d})^{-1}\big)^2\Big)^{1/2}=\frac{\delta}{2},\] which is impossible!
-
Let \(\mathcal Q_1= \{Q\in \mathcal Q:Q\cap E_1\neq\varnothing\}\) and \(\mathcal Q_2= \{Q\in \mathcal Q:Q\cap E_2\neq\varnothing\}\). Consequently, we obtain that \[\begin{aligned} \sum_{k\in\mathbb N}{\rm v}_d(R_{k})&=\sum_{n\in\mathbb N}{\rm v}_d(Q_n)\\ &\ge \sum_{Q\in \mathcal Q_1}{\rm v}_d(Q)+ \sum_{Q\in \mathcal Q_2}{\rm v}_d(Q)\\ &\ge \lambda_d^*(E_1)+ \lambda_d^*(E_2). \end{aligned}\]
This competes the proof. $$\tag*{$\blacksquare$}$$